二叉树理论基础
相关代码用golang编写
数据结构
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
二叉树是每个节点最多能拥有两个子树的树结构，通常子树被称为左子树和右子树，二叉树常用于实现二叉查找树
基本概念：
- 叶子节点是指没有子节点的节点
- 深度：深度是指根节点到该节点的最长简单路径边条数
- 高度：深度是指该节点到叶子结点的最长简单路径边条数
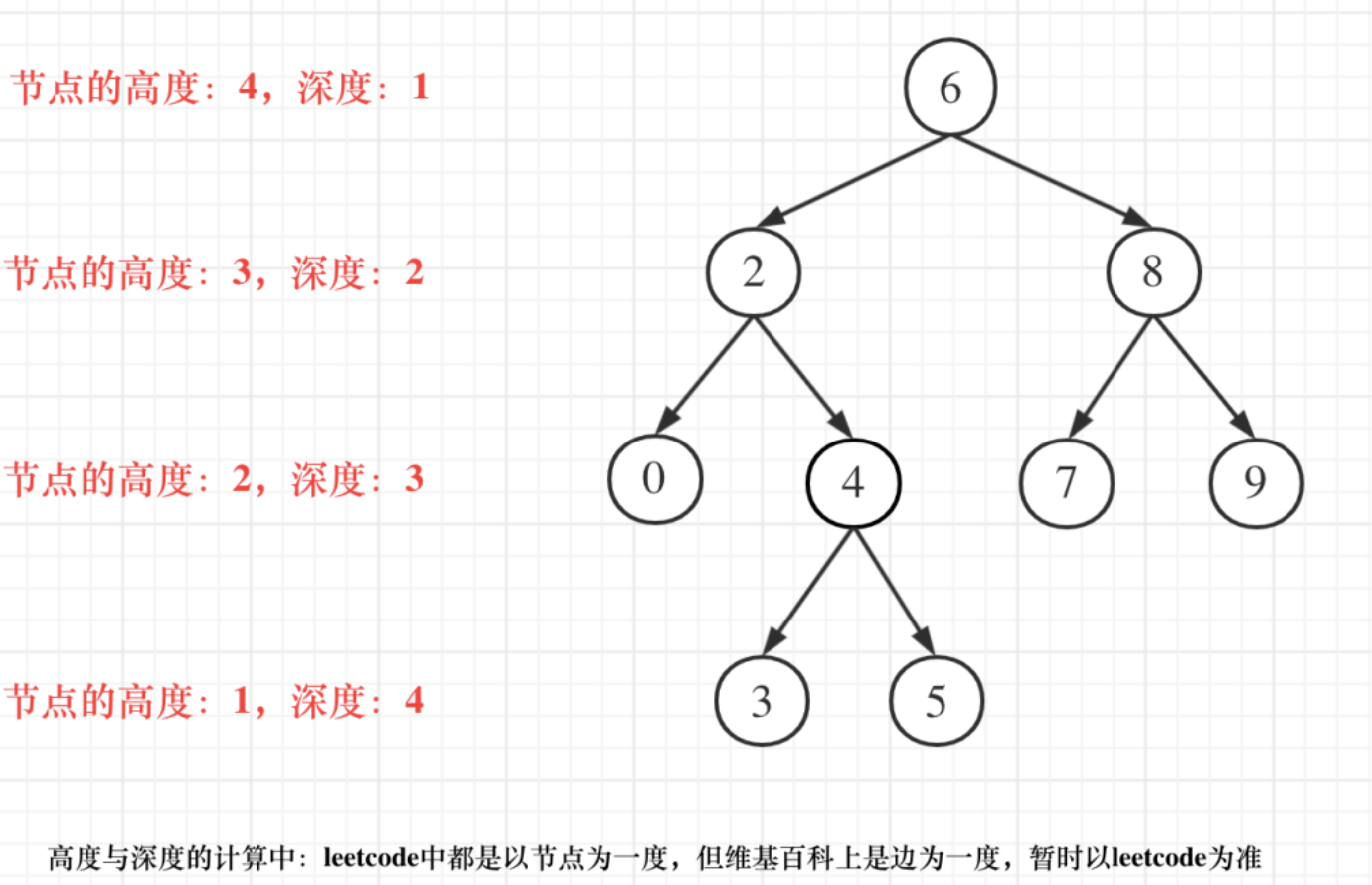对于根节点的深度为0还是1，需要看环境的定义
二叉树种类说明：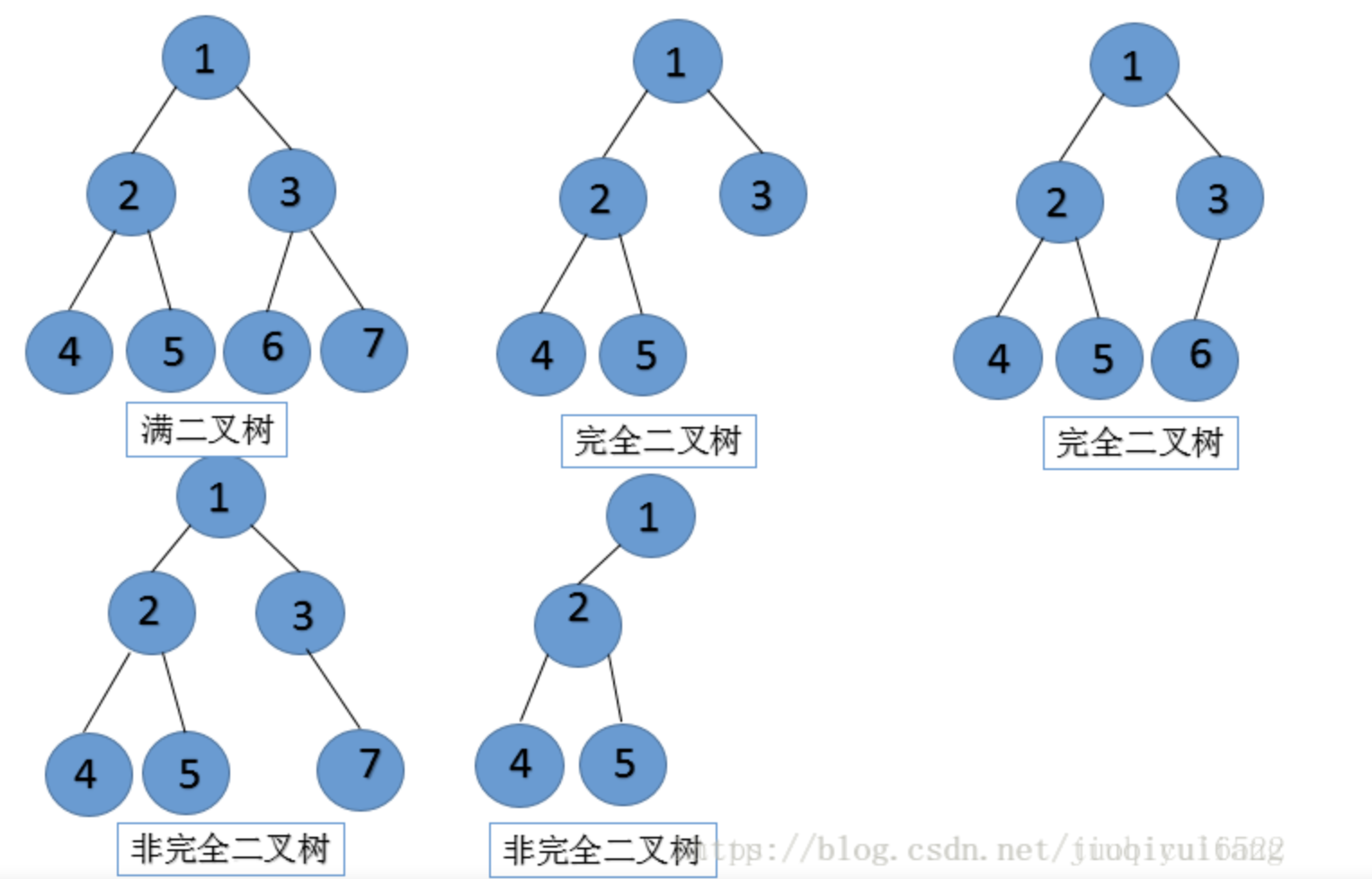 
对于根节点的深度为0还是1，需要看环境的定义
- 完全二叉树——叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。
- 满二叉树——叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树，他是一种特殊的完全二叉树。
- 平衡二叉树——具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
二叉树遍历
- 前序遍历（深度优先，递归，迭代）
- 中序遍历（深度优先，递归，迭代）
- 后序遍历（深度优先，递归，迭代）
- 层序遍历（广度优先，迭代）
遍历说明
对于二叉树的遍历顺序来说，都是针对中间节点的顺序
前序遍历
即中左右顺序（按照中间节点，左子树，右子树顺序）
递归方式：
func preorderTraversal(root *TreeNode) []int {
var res []int
var dfs = func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
res = append(node.Val)
dfs(node.Left)
dfs(node.Right)
}
dfs(root)
return res
}
中序遍历
即左中右
func inorderTraversal(root *TreeNode) []int {
var res []int
var dfs = func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
dfs(node.Left)
res = append(node.Val)
dfs(node.Right)
}
dfs(root)
return res
}
后序遍历
即左右中 ``` func postorderTraversal(root *TreeNode) []int {
var res []int
var dfs = func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
dfs(node.Left)
res = append(node.Val)
dfs(node.Right)
}
dfs(root)
return res } ```
层序遍历
即一层一层的读取数据，这里要利用到队列来实现，将每一层的节点放到队列中再按照每层的长度将队列数据依次取出直到队列为空
fucn breadthFirst(root *TreeNode) [][]int {
if root == nil {
return [][]int {}
}
var res [][]int
var tmp []int
var queue []*TreeNode
queue = append(queue, root)
for len(queue) != 0 {
length := len(queue)
for i := 0; i < length; i++ {
node := queue[0]
queue = queue[1: len(queue)]
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
tmp = append(tmp, node.Val)
}
res = append(res, tmp)
tmp = []int{}
}
return res
}
二叉树创建
- 通过遍历顺序创建
获取二叉树层数
递归
递归使用后序遍历的方式求节点高度，而根节点高度即二叉树最大深度，即调用该函数时传入根节点即可
func getHeight(node *TreeNode) int {
// 遍历到空节点时即高度为0
if node == nil {
return 0
}
// 中序遍历的目的是最后处理中间节点，将当层的处理结果返回给父节点
leftHeight := getHeight(node.Left)
rightHeight := getHeight(node.Right)
// 当前节点高度为
height := max(leftHeight, rightHeight) + 1
return height
}
- 迭代(层序遍历)
非递归方式可以直接按层序遍历的思路记录层数
fucn layers(root *TreeNode) int {
if root == nil {
return [][]int {}
}
var res int
var queue []*TreeNode
queue = append(queue, root)
for len(queue) != 0 {
res++
length := len(queue)
for i := 0; i < length; i++ {
node := queue[0]
queue = queue[1: len(queue)]
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
}
return res
}
文档信息
- 本文作者：Mikatsuki
- 本文链接：https://akitozz.github.io/2022/10/23/binarytree-1/
- 版权声明：自由转载-非商用-非衍生-保持署名（创意共享3.0许可证）